Home 알고리즘 대회에 필요한 수학
Post
Cancel

알고리즘 대회에 필요한 수학

Posted Aug 17, 2022
By syshin
views 41 min read

출처: 알고리즘 대회에 필요한 수학

알고리즘 대회에 필요한 수학

이산 수학

점화식 풀이 기법들

  • 2차 선형동차점화식 (Linear homogenous recurrence)
    • 다음과 같은 형태: ak=α⋅ak−1+β⋅ak−2a_{k} = \alpha \cdot a_{k-1} + \beta \cdot a_{k-2}.
    • an=rna_{n}=r^{n} 꼴이라고 생각하고 대입해 보면 r2−α⋅r−β=0r^{2} - \alpha\cdot r - \beta = 0을 얻는다. 이 방정식의 해 rr에 대해 rnr^{n}은 해가 됨.
    • 해가 둘 있을 경우, a⋅r1n+b⋅r2na\cdot r_{1}^{n} + b\cdot r_{2}^{n} 꼴의 선형 결합도 해가 된다 (당연). 이 계수들을 초기상태에 맞도록 지정.
    • Application:
      • 피보나치 수열의 일반항은?
      • pp의 확률로 이기는 bet을 한다. (승-패)가 WW가 되거나 −L-L이 될 때까지 하는데, 이 때 WW 승으로 끝날 확률은? (ICPC WF '13 B)
    • 일반화: 3차, 4차, 5차.. 라도 같은 요령으로 풀 수 있다 (3차, 4차 방정식을 풀기 힘들어서 그렇지)
      • 중근이면 어떻게? 만약 rr이 m+1m+1번 중근으로 등장한다면 rn,n⋅rn,⋯,nm⋅rnr^{n}, n\cdot r^{n}, \cdots, n^{m}\cdot r^{n} 의 선형결합이 들어간다.

  • 선형비동차점화식 (Linear non-homogenous recurrence)

    • ak=αk−1ak−1+⋯+αk−nak−n+f(n)a_{k} = \alpha_{k-1}a_{k-1} + \cdots + \alpha_{k-n}a_{k-n} + f(n) (마지막의 f(n)f(n)에 주의!)
    • 해법
      • an=bn+hna_n = b_n + h_n으로 분해 (bnb_n은 점화식만 만족하고 초기상태는 만족하지 않는 답. 대개 f(n)f(n)과 비슷한 형태를 갖는다.
      • hnh_n을 찾고 ana_n의 계수를 초기상태 성립하도록 맞춰 주면 됨.

  • 간단한 정리

  • 일반항 계산을 직접 하는 경우도 있지만 행렬의 형태로 표현하고 푸는 일이 많다.

    • 예) 피보나치 수열의 n번째 수를 구하기 위해서는 [Fn+2Fn+1]=(1110)[Fn+1Fn]\begin{bmatrix} F_{n+2} \\ F_{n+1} \end{bmatrix} = \begin{pmatrix} 1 & 1\\ 1 & 0 \end{pmatrix} \begin{bmatrix} F_{n+1} \\ F_{n} \end{bmatrix} 의 점화식으로부터 얻는 다음의 식을 이용해 계산한다. (1110)n[10]\begin{pmatrix} 1 & 1\\ 1 & 0 \end{pmatrix}^n \begin{bmatrix} 1 \\ 0 \end{bmatrix}

이항계수와 숫자 세기

  • 이항계수 (Binomial coefficient): nCr=(nr)=n!(n−r)!r!nCr = \left ( n \atop r \right ) = \frac{n!}{(n-r)!r!}
    • 점화식: (nr)=(n−1r−1)+(n−1r)\left( n \atop r \right ) = \left( n-1 \atop r-1 \right) + \left( n-1 \atop r \right)
    • Identity: (n0)=(nn)=1\left( n \atop 0 \right ) = \left ( n \atop n \right ) = 1, ∑i=0n(ni)=2n\sum_{i=0}^{n}\left(n \atop i\right) = 2^{n}.
  • 이항계수를 이용해 순열 수 세기: nn개의 원소 중에서 rr개를 뽑을 수 있는 경우의 수는?
    • 유의해야 할 것
      • 중복 여부: 같은 원소를 두 번 뽑을 수 있는가?
      • 순서 여부: 같은 원소를 순서만 다르게 뽑았으면 다른 경우로 치는가?
    • 공식
      • 중복 없이, 순서 있을 때: n!(n−r)!=nPr\frac{n!}{(n-r)!} = nPr
      • 중복 있고, 순서 있을 때: nrn^{r}
      • 중복 없이, 순서 없을 때: (nr)\left ( n \atop r \right)
      • 중복 있고, 순서 없을 때: (n+r−1r)\left ( n + r - 1 \atop r \right ) (nn개의 원소와 r−1r-1개의 막대기를 내려놓는 방법의 수)
  • 카탈란 수: 다양한 문제의 답이 된다.
    • 예제 문제들: 길이가 2n인 괄호 수식의 수, n+1개의 리프를 가진 풀 바이너리 트리의 수, etc.
    • 수식: Cn=1n+1(2nn)C_n = \frac{1}{n+1} \left( 2n \atop n \right )
  • Multinomial coefficient
  • 탑코더 튜토리얼

포함-배제 법칙

  • 교집합이 있는 n개의 집합의 합집합의 크기를 구하려면:
    • 각 집합의 크기를 모두 더한다.
    • 각 2개 집합에 대해 교집합의 크기를 모두 뺀다.
    • 각 3개 집합에 대해 교집합의 크기를 모두 더한다.
    • ...
  • 탑코더 튜토리얼
  • Application: Derangement 계산하기 - n개의 원소를 섞되, 그 중 아무 것도 원래 위치에 있지 않는 경우의 수는?
    • Let: AiA_i = ii가 제 자리로 간 순열의 개수.
    • ∑i=0n(−1)n−i(ni)i!\sum_{i=0}^{n}(-1)^{n-i}\left( n \atop i \right)i!
  • Moebius 함수와 반전 공식 - 약수/배수 관계를 이용한 포함-배제 법칙이 필요한 경우 이 함수로 답이 나타날 수 있다.
    • n 이하의 Square Free 개수 세기 - ∑i∈Z+μ(i)⌊ni2⌋\sum_{i \in \Bbb{Z}^+} \mu (i) \lfloor \frac{n}{i^2} \rfloor가 답이 된다. n\sqrt{n}까지만 계산해주면 원하는 개수가 나온다.

번사이드 정리

  • 페트르님의 정리
  • 경우의 수를 세는데, 특정 transform operation(회전, 반사, ..)해서 같은 경우들은 하나로 친다. 전체 경우의 수는?
    1. 각 operation마다 이 operation을 했을 때 변하지 않는 경우의 수를 센다 (단, "아무것도 하지 않는다"라는 operation도 있어야 함!)
    2. 전체 경우의 수를 더한 후, operation의 수로 나눈다. (답이 맞다면 항상 나누어 떨어져야 한다)
  • Application:
    • n×nn\times n (nn은 편의를 위해 짝수) 크기의 격자를 xx개의 색깔로 칠하는 경우의 수는? 단 회전해서 같은 경우는 같은 것으로 친다.
      • 아무것도 하지 않을 때: 모든 격자가 변하지 않는다. xn∗nx^{n*n}
      • 90도 회전, 270도: 4개씩 칸을 그룹지어, 각 그룹은 같은 색이어야 한다. 따라서 xn∗n/4x^{n*n/4}
      • 180도 회전: 2개씩 칸을 그룹지어, 각 그룹은 같은 색이어야 한다. 따라서 xn∗n/2x^{n*n/2}개의 경우의 수
    • 최종 답은 이들의 평균!
    • 만약 nn이 홀수라면 어떨까?

키르히호프 정리

  • 그래프의 생성 수형도(흔히 말하는 스패닝 트리)의 경우의 수를 구하는 정리로 대수적 그래프 이론에서 공부하게 된다.
  • 무향 그래프의 Laplacian matrix LL를 만든다. 간단히 설명하면 (정점의 차수 대각 행렬) - (인접행렬)이다. LL에서 행과 열을 하나씩 제거하고 이것을 L∗L^*라 하자. 어느 행/열이든 관계 없다. 그래프의 생성 수형도의 개수는 det(L∗)\det (L^{*})이다.
  • 예제: K4\rm{K}_4의 Laplacian matrix는 [3−1−1−1−13−1−1−1−13−1−1−1−13]\begin{bmatrix} 3 & -1 & -1 & -1 \\ -1 & 3 & -1 & -1 \\ -1 & -1 & 3 & -1 \\ -1 & -1 & -1 & 3 \\ \end{bmatrix} 이다. 여기서 첫번째 행과 첫번째 열을 제거하면 [3−1−1−13−1−1−13]\begin{bmatrix} 3 & -1 & -1 \\ -1 & 3 & -1 \\ -1 & -1 & 3 \\ \end{bmatrix} 이고 가우스 조단 방법을 쓰면 [111040004]\begin{bmatrix} 1 & 1 & 1 \\ 0 & 4 & 0 \\ 0 & 0 & 4 \\ \end{bmatrix} 이 되어서 1×4×4=161 \times 4 \times 4 = 16으로 우리가 알고 있던 Cayley 정리에 의한 답인 44−2=164^{4-2} = 16과 같다.

생성함수

  • 제대로 이 토픽을 다룰 필요는 없지만 경우의 수 문제를 다룰 때 쓰이는 경우가 있다.
  • 1원짜리 동전 5원짜리 동전 8원짜리 동전을 이용해서 몇억원을 만드는 경우의 수를 구한다고 하자.
    • (1+x+x2+⋯)(1+x5+x10+⋯)(1+x8+x16+⋯)(1 + x + x^2 + \cdots) (1 + x^5 + x^{10} + \cdots) (1 + x^8 + x^{16} + \cdots)를 전개하면 x몇억x^{몇억}의 계수가 답이 된다.
    • 생성함수에서 해당 식은 1(1−x)(1−x5)(1−x8)\frac{1}{(1-x)(1-x^5)(1-x^8)}으로 표현할 수 있다.
    • 계산을 위해 다음을 생각해보자. 1,5,8의 최소공배수인 40을 써서 (1−x40)3(1-x^{40})^3을 곱하면 (1+x+⋯+x39)(1+x5+⋯+x35)(1+x8+⋯+x32)(1+x+\cdots+x^{39})(1+x^5+\cdots+x^{35})(1+x^8+\cdots+x^{32})이다. 해당 식의 분자와 분모에 (1−x40)3(1-x^{40})^3을 곱하는 것을 생각해주면 된다. 분자는 106차식이다. 107개 항으로 쪼개고 분모의 (1−x40)3(1-x^{40})^3으로부터 얻어지는 계수를 곱해주고 더하면 원하는 답을 얻는다.
      • 분모로부터 얻어지는 계수는 ∑(n+22)x40n=1(1−x40)3\sum{ {n+2 \choose 2} x^{40 n} } = \frac{1}{(1-x^{40})^3}에서 얻는다. 이렇게 되면 항상 40의 배수이므로 유효하게 고려하는 항의 개수는 약 140\frac{1}{40}으로 줄어든다.
    • 이 예제처럼 터무니 없이 큰 범위에 대해 답을 계산해야할 때는 수식만 잘 다룰 줄 알면 쉽다. SRM 600.5의 1000점 문제는 이러한 방식으로 풀린다.
  • 어떤 수열의 점화식을 알 때 수열의 합을 구할 때도 쓸 수 있다. ∑anxn\sum{a_n x^n} 꼴로 우리가 원하는 답이 표현되는 경우에 적용할 수 있다.
    • 피보나치 수열의 power series가 유명한 예이다. s(x):=∑Fnxn=x1−x−x2s(x) := \sum{F_n x^n} = \frac{x}{1-x-x^2}임을 s(x) 정의와 점화식에서 얻을 수 있다. x가 수렴하는 범위(황금비의 역수보다 절대값이 작은 경우)에 있기만 하면 된다.
  • 읽어볼만한 pdf 링크

게임이론

스프라그-그룬디 정리

  • 튜토리얼 링크, 탑코더 튜토리얼, 또다른 튜토리얼
  • Nim 게임
    • 규칙
      • 조약돌 kk 무더기가 있다고 하자. 각 무더기에 포함된 조약돌의 개수는 다를 수 있다.
      • 각 플레이어는 무더기를 하나 선택해서 그 무더기에서 1개 이상의 조약돌을 가져온다. (무더기에 남은 조약돌을 전부 가져와도 된다.)
      • 마지막 조약돌을 가져가는 플레이어가 승리한다.
    • Nim 게임의 해법
      • 각 무더기의 조약돌 수를 전부 XOR한다. 0이면 패배! 0 이상이면 승리!
  • 일반화하기:
    • 모든 impartial(어느 플레이어든지 놓을 수 있는 수가 같다), normal play(마지막에 수를 두는 사람이 이긴다) 게임은 비슷한 해법으로 풀 수 있다.
      • 다음과 같은 규칙:
        • 게임은 한 개 이상의 서브게임으로 구성된다.
        • 각 서브게임은 상태들의 DAG로 구성된다.
        • 각 플레이어는 하나의 서브게임을 골라 해당 서브게임의 상태를 한 번 움직인다.
        • 더 이상 움직일 수 없는 사람이 진다.
    • 어떻게 풀까?
      • 게임의 각 상태에 대해 Grundy 수를 계산한다.
      • 우선 하나의 서브게임만 보자.
        • 지는 상태(마지막 상태)의 Grundy 수는 0이다.
        • 그 외의 상태에서는 이 상태에서 나가는 상태들의 Grundy 수를 모은 뒤, 그 중에 포함되지 않은 가장 작은 0 이상의 정수(minimum excluded number)가 Grundy 수가 된다.
      • 여러 개의 서브게임이 있다면 각 서브게임의 상태를 XOR한다.
    • Nim에서는: nn개의 조약돌이 남아있다면 Grundy 수는 nn
  • Application: fill in!

확률론

기대값의 선형성

  • E(∑iAi)=∑iE(Ai)E(\sum_{i}A_i) = \sum_i E(A_i)
  • 당연한 얘기같지만 가끔 예상치 못한 간단한 답을 준다! 합을 어떻게 나누느냐에 따라 중요.
  • Application
    • N+1N+1층짜리 건물의 1층에 엘리베이터가 섰는데, MM명이 탔다. 각 사람이 가는 층은 랜덤하게 결정된다. 엘리베이터가 서는 횟수의 기대값은?
      • 각 층별로 설 때 1이 되는 indicator function의 기대치를 구해서 더한다.
    • 또 다른 예제: 평면상에 NN개의 점이 있다. 각 점마다 해당 점이 존재하거나 지워질 확률이 주어진다. Convex hull 넓이의 기대값은?
      • 각 간선별로 외적값의 기대치를 더한다.

정수론

모듈라 연산

  • N으로 나눈 결과값을 구할 때, 연산 중간 결과도 N으로 나눠도 된다.
    • (a+b)modN=(amodN+bmodN)modN(a + b) \mathrm{mod}N = (a \mathrm{mod}N + b\mathrm{mod}N) \mathrm{mod}N
    • (a−b)modN=(amodN−bmodN+N)modN(a - b) \mathrm{mod}N = (a \mathrm{mod}N - b\mathrm{mod}N + N) \mathrm{mod}N
    • (a∗b)modN=(amodN∗bmodN)modN(a * b) \mathrm{mod}N = (a \mathrm{mod}N * b\mathrm{mod}N) \mathrm{mod}N
  • 단 나눗셈에는 성립하지 않는다. aa로 나누기 위해서는, 곱셈의 역원을 대신 곱해줘야 한다. 모듈라 곱셈의 역원은 두 가지 방법으로 구할 수 있다.
    • 한 가지 방법은 오일러 정리를 이용하는 것이다.
      • aϕ(N)≡1(modN)a^{\phi(N)} \equiv 1 (\mathrm{mod}N)
      • 이 때 phi(N)phi(N)은 오일러 피 함수. 아래를 참조하라. 단 이거 계산하는건 배보다 배꼽이 더 클 수도.
      • NN이 소수라면 ϕ(N)=N−1\phi(N)=N-1이니 aN−2a^{N-2}을 계산하여 역원을 얻을 수 있다.
      • 이것을 거듭제곱 빨리 구하기로 구하면 된다.
    • 두번째 방법(아마 더 효율적)은 확장 유클리드 알고리즘을 쓰는것이다. 아래를 참조하라.
    • [1..N][1..N]구간에 대해서 각각의 역원을 미리 계산해 둬야 한다면, DP를 이용해 O(N)O(N)에 구하는 방법도 있다. codeforces 링크를 참조. pp에 대해서 구할 경우, 점화식은 다음과 같다.
      • inv(i)=(p−[p/i])∗inv(pmodi)modpinv(i)=(p-[p/i])*inv(p \mathrm{mod}i) \mathrm{mod} p

확장 유클리드 알고리즘

  • 목적: 상수 aa, bb에 대해 ax+by=gcd(a,b)ax + by = \mathrm{gcd}(a, b)를 만족하는 xx, yy를 찾아준다.
  • Naive derivation:
    • 유클리드 gcd 알고리즘에서, gcd()gcd()의 입력이 되는 숫자들은 항상 최초 숫자들의 선형 결합으로 표현할 수 있다.
    • 따라서 각 숫자 aa와 bb를 넘길 때, 이들을 최초 숫자들의 선형 결합으로 표현한 방법 또한 넘겨주면 간단하게 풀 수 있다.
    • 물론 이대로 구현하면 아주 귀찮다. 대신에 gcd(a,b)gcd(a, b) 함수가 최대공약수와 함께 ax+by=gax+by=g 의 해 xx, yy를 반환하도록 하면 쉽게 풀 수 있다.

C++ 구현

struct Solution { int gcd, x, y; };
Solution extendedEuclid(int a, int b) {
  int q = a / b, r = a % b;
  if(r == 0) return Solution{b, 0, 1}; 
  Solution s = extendedEuclid(b, r);                                                                                                            
  // now, we have
  // s.gcd = s.x * b + s.y * r
  //       = s.x * b + s.y * (a - q * b)
  //       = s.y * a + (s.x - q * s.y) * b
  return Solution{s.gcd, s.y, s.x - q * s.y};
}
  • Application:
    • 위에서 얘기했듯이, 모듈라 연산에서 곱셈의 역원 구하기. modN\mathrm{mod } N인 모듈로 연산을 할 때, aa와 NN이 서로소라 하자. (NN이 소수면 항상 참) 따라서 aa와 NN의 egcd 결과는 항상 ax+Ny=1ax + Ny = 1이 된다. NN로 나눠보면 ax=1(modN)ax = 1 (\mathrm{mod }N). 따라서 xx는 aa의 곱셈 역원이다. (단, 결과값이 음수라면 NN을 더해줘야 함)

중국인 나머지 정리

뤼카의 정리

  • 음이 아닌 정수 mm, nn과 임의의 소수 pp에 대해 (mn)(modp){m \choose n}\pmod p를 계산하는 정리이다.
  • mm과 nn을 pp진법으로 전개하여 그 p진 숫자를 mim_i와 nin_i라고 하자. 자리수가 다르면 0을 채워넣어 맞춰준다. 그러면 (mn)≡∏(mini)(modp){m \choose n}\equiv\prod{m_i \choose n_i}\pmod p이다.
  • 이 때 mi<nim_i < n_i이면 (mini)=0{m_i \choose n_i} = 0으로 취급한다.

오일러 피 함수, 약수의 합(시그마) 함수, 약수의 개수 함수, 뫼비우스 함수

  • 이 함수들은 서로소인 것들에 대해 multiplicative 함수들이기 때문에 n 이하의 모든 값을 계산해야할 경우 에라토스테네스의 체를 이용하면 O(n log n)에 된다.
  • 오일러 피 함수는 자신보다 작은 서로소인 정수의 개수를 나타내는 함수이다.
    • φ(n)=n∏p∣n(1−1p)\varphi(n) =n \prod_{p\mid n} \left(1-\frac{1}{p}\right)이고, 소인수 분해한 경우를 생각하면 계산하기 쉽다.
  • 어떤 정수가 있을 때, pip_i를 소인수라고 하고 aia_i를 pip_i 소인수의 거듭제곱 횟수라고 하자. 약수의 합(x=1), 약수의 개수(x=0) 함수는 ∏(1+pix+⋯+pixai)\prod(1+p_i^{x}+\cdots+p_i^{x a_i})로 계산할 수 있다.
  • 뫼비우스 함수는 ∑d|nμ(d)={1 if n=10 if n>1.\sum_{d | n} \mu(d) = \begin{cases}1&\mbox{ if } n=1\\ 0&\mbox{ if } n>1.\end{cases}를 사용해 계산할 수 있다.
  • 이 함수들의 관계는 위키피디아 링크를 참고

분할 정복을 이용한 빠른 수식 계산

빠른 거듭 제곱 계산

  • 분할 정복:
    • x2n=(xn)⋅(xn)x^{2n} = (x^n) \cdot (x^n)
    • x(2n+1)=x⋅x2nx^{(2n+1)} = x \cdot x^{2n}

빠른 등비 수열의 합

  • 분할 정복:
    • A2n+A2n−1+A2n−2+⋯+A1A^{2n} + A^{2n-1} + A^{2n-2} + \cdots + A^{1}
    • =(A2n+An)+(A2n−1+An−1)+⋯= (A^{2n} + A^{n}) + (A^{2n-1} + A^{n-1}) + \cdots
    • =(1+An)(An+An−1+⋯+A1)= (1 + A^n)(A^{n} + A^{n-1} + \cdots + A^{1})

행렬의 합

  • 수열에 대한 테크닉을 바로 쓸 수도 있지만 I−AI-A의 역행렬이 있는 경우에는
    • I+A+A2+⋯+An−1=(I−An)(I−A)−1\begin{align} I + A + A^2 + \cdots + A^{n-1} & = (I - A^n)(I-A)^{-1}\\ \end{align}
    • 무한히 더해야 할 때, 합이 수렴하는 경우 (I−A)−1(I-A)^{-1}이 답이 된다.

선형 시스템

가우스 소거법

  • 가우스 소거법은 역행렬 계산, determinant 계산, 일차연립방정식 풀이 등에 쓸 수 있는 방법을 정리한 것이다. 행렬의 rank는 변하지 않는 연산들로 이뤄져 있다. 최종 목적은 row echelon form 또는 대각행렬로 만드는 경우가 많다.
  • 사용할 수 있는 연산
    1. 어떤 값 k를 원하는 행 하나를 택하여 곱한 결과를 다른 행에 더한다. 가장 기본이 되는 연산이고 determinant는 보존된다.
      • 예제: (341552)\begin{pmatrix} 3 & 4 & 1 \\ 5 & 5 & 2 \end{pmatrix} 에 첫번째 행에 -2를 곱하고 두번째 행에 더하여 (341−1−30)\begin{pmatrix} 3 & 4 & 1 \\ -1 & -3 & 0 \end{pmatrix} 을 얻는 작업을 해볼 수 있다.
      • 이 예제의 작업을 matrix 곱으로 표현하면 다음과 같다. 행렬 determinant는 multiplicative이므로(detAB=detA⋅detB\det{AB} = \det{A} \cdot \det{B}) 다음의 등식에서 determinant가 보존되는 것을 확인할 수 있다.
        • (10−21)(341552)=(341−1−30)\begin{pmatrix} 1 & 0 \\ -2 & 1 \end{pmatrix} \begin{pmatrix} 3 & 4 & 1 \\ 5 & 5 & 2 \end{pmatrix} = \begin{pmatrix} 3 & 4 & 1 \\ -1 & -3 & 0 \end{pmatrix}
    2. 어떤 값 k를 원하는 행 하나를 택하여 곱해준다. 이 연산의 결과로 행렬의 determinant는 k배가 된다.
      • 첫번째 행을 k배 한다고 하면 다음과 같은 행렬을 곱해준 것으로 생각할 수 있다. (k0⋯001⋯0⋮⋮⋱⋮00⋯1)\begin{pmatrix} k & 0 & \cdots & 0\\ 0 & 1 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}
    3. 원하는 행 두 개를 바꿔준다. 이 연산의 결과로 행렬의 determinant는 -1배가 된다.
      • 첫째 행과 둘째 행을 교체한다고 하면 다음과 같은 행렬을 곱해준 것으로 생각할 수 있다. (01⋯010⋯0⋮⋮⋱⋮00⋯1)\begin{pmatrix} 0 & 1 & \cdots & 0\\ 1 & 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}
  • 사용하는 방법
    • 역행렬: 대상 행렬에 해주는 작업을 단위행렬에 똑같이 해주되 대상 행렬을 단위행렬로 만들면 같은 작업을 적용해줬던 단위행렬은 역행렬로 바뀌어 있다.
      • (2312)\begin{pmatrix} 2 & 3 \\ 1 & 2 \end{pmatrix} 를 단위행렬로 만드는 연산의 예제는 다음과 같다.
        • 2번 행을 1번 행에서 뺀다. 1번 행은 1 1이 된다.
        • 1번 행을 2번 행에서 뺀다. 2번 행은 0 1이 된다.
        • 2번 행을 1번 행에서 뺀다. 1번 행은 1 0이 된다.
      • 해당 작업을 단위행렬에 똑같이 순서대로 해주면 (2−3−12)\begin{pmatrix} 2 & -3 \\ -1 & 2 \end{pmatrix}이 된다.
    • determinant를 구할 때도 쓸 수 있다. 키르히호프 정리의 예제처럼 삼각형 모양이면 대각선을 곱해주는 것으로 계산할 수 있다. 그러한 구하기 쉬운 모양으로 변환해주면서 determinant가 어떻게 변해왔는지 기억하면 원래 행렬의 determinant를 계산할 수 있다.
    • 일차연립방정식 풀이
      • 연립방정식을 행렬로 표현한다. mm개의 연립 방정식에 변수가 nn개라고 하자. 계수를 의미하는 m×nm \times n짜리 행렬 AA와 변수 nn개를 의미하는 n×1n \times 1짜리 열 벡터 xx와 남은 상수항을 의미하는 열 벡터 bb를 생각하면 Ax=bAx = b로 연립일차방정식을 표현할 수 있다.
      • 양 변에 똑같은 작업을 해주면서 좌측의 행렬을 단위행렬처럼 만들면 x를 알 수 있다.
    • 원하는 모양을 만들기 위한 전략으로는 다음의 것이 많이 쓰인다.
      • 0행 0열의 원소를 1로 만들어주고 i행 0열의 원소를 0으로 만들어준다.
      • 1행 1열의 원소를 1로 만들어주고 i행 1열의 원소를 0으로 만들어준다.
      • 행렬의 끝에 도달할 때까지 대각선을 1로 만들고 나머지를 0으로 만드는 작업을 계속 반복하여 단위행렬을 얻는다.
      • 항상 대각선을 1로 만들 수 있는 것은 아니다. 그러한 경우 1로 만들 위치는 오른쪽으로 한 칸 옮겨서 진행한다. 그렇게 작업한 경우 row echolon form이 된다.

심플렉스법

  • 진짜로 이거 필요할까? -_-

리니어 시스템과 플로우

기초 수치 해석

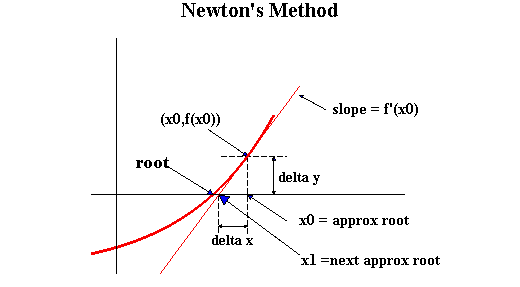
Newton method

  • 가장 기초적인 근 찾기(root-finding) 알고리즘. f(x)f(x)와 f′(x)f'(x)의 구현이 주어질 때, f(x)=0f(x)=0인 위치를 찾는다.
  • 처음에 답이 x0x_0이라고 찍어보자. f(x0)f(x_0)을 계산해보니 0이 아니었다. 그러면 어떻게 할까?
  • 좋은 방법은 f(x)f(x)를 선형함수로 근사하고, 이 경우 해가 되는 위치가 어디일지를 찾는 것이다. 다음 그림을 참조하자. (출처

C++ 구현

// f(x)와 f'(x), 초기값이 주어졌을 때 해를 찾는다.
template<typename Function1, typename Function2>
double newton(Function1 f, Function2 fp, double init, double tolerance=1e-8, int iterations=10000) {
  double x = init;
  while(iterations--) {
    double fx = f(x);
    if(fabs(fx) < tolerance) return x;

    double fpx = fp(x);
    x -= fx / fpx;
  }
  // did not converge!
  return x;
}

Adaptive Simpson 수치 적분

  • f(x)f(x) 함수의 구현이 주어질 때, 해당 함수를 여러번 호출해서 해당 함수의 부정적분 없이도 정적분을 계산하는 기법들.
    • Simpson법은 해당 함수를 2차함수로 근사해서 적분한다. 따라서 해당 함수가 2차 이하라면 항상 정확한 답이 나온다.
    • Adaptive Simpson 적분 알고리즘은 해당 함수가 2차 함수에서 얼마나 벗어나는지 확인하고, 많이 벗어난다면 분할 정복한다. 자세한 백그라운드는 나도 모르니 싣지 않는다. 구현은 다음과 같다.

C++ 구현

template<typename Function>
double simpson(Function f, double a, double b) {
  double c = (a + b) / 2.0;
  double h3 = fabs(b - a) / 6.0;
  return h3 * (f(a) + 4.0 * f(c) + f(b));
}

// sum은 처음에 simpson(f, a, b)로 초기화한다.
// 오차가 eps 이상으로 추정되는 경우 분할정복한다.
template<typename Function>
double adaptiveSimpson(Function f, double a, double b, double sum, double eps) {
  double c = (a + b) / 2.0;
  double left = simpson(f, a, c);
  double right = simpson(f, c, b);
  if(fabs(left + right - sum) <= 15 * eps) 
    return left + right - (left + right - sum) / 15;
  return adaptiveSimpson(f, a, c, left, eps/2) + adaptiveSimpson(f, c, b, right, eps/2);
}

긴 정수 곱셈

카라츠바 알고리즘

  • 카라츠바 알고리즘은 긴 정수 둘을 곱하는 분할 정복 알고리즘이다. BB진수 nn자리 긴 정수 aa, bb를 곱한다고 하자. (nn은 2의 자승으로 가정한다.)
  • 이 때 두 숫자를 모두 절반(n/2n/2 자리씩)으로 다음과 같이 자르자.
    • a=a1×Bn/2+a0a = a_{1} \times B^{n/2} + a_{0}
    • b=b1×Bn/2+b0b = b_{1} \times B^{n/2} + b_{0}
  • 이 때 다음과 같이 두자.
    • z0=a0×b0z_0 = a_0 \times b_0
    • z2=a1×b1z_2 = a_1 \times b_1
    • z1=(a0+a1)×(b0+b1)−z0−z1=a0×b1+a1×b0z_1 = (a_0 + a_1) \times (b_0 + b_1) - z_0 - z_1 = a_0 \times b_1 + a_1 \times b_0
  • 그러면
    • a⋅b=(a1⋅Bn/2+a0)⋅(b1⋅Bn/2+b0)=(a1⋅b1)⋅Bn+(a0⋅b1+a1⋅b0)⋅Bn/2+(a0⋅b0)a \cdot b = (a_1 \cdot B^{n/2} + a_0) \cdot (b_1 \cdot B^{n/2} + b_0) = (a_1 \cdot b_1) \cdot B^{n} + (a_0 \cdot b_1 + a_1 \cdot b_0) \cdot B^{n/2} + (a_0 \cdot b_0)
    • =z2⋅Bn+z1⋅Bn/2+z0= z_2 \cdot B^{n} + z_1 \cdot B^{n/2} + z_0
  • BnB^{n}으로의 곱은 선형시간에 할 수 있다는 점을 감안하면, n/2n/2 크기의 정수 곱셈 세 번만 하면 되기 때문에 확실히 빠르다!

FFT와 다항식 곱셈

  • 빠른 다항식 곱셈 알고리즘이 있으면 긴 정수 곱셈도 빠르게 할 수 있다. 긴 정수를 몇 자리씩 끊어서 다항식의 계수로 삼은 뒤, 두 다항식을 곱하고, 마지막에 올림 처리만 해 주면 되기 때문.
  • 다항식 곱셈 또한 물론 단순한 방법은 O(n2)O(n^2)인데, FFT를 이용하면 O(nlg⁡n)O(n \lg n)에 할 수 있다.
  • FFT 곱셈은 다항식에 두 가지 표현 방식이 있다는 것을 이용한다:
    • 계수 목록 형태: 대부분 사용하는 방식
    • x, y쌍 형태: 2n2n개의 상수 x0,x1,⋯,xn−1x_0, x_1, \cdots, x_{n-1}에 대해 f(x0),f(x1),⋯f_(x_0), f_(x_1), \cdots를 저장하는 방식
  • nn개의 샘플은 nn차 방정식을 유니크하게 정의하기 때문에 이 두 표현 방식은 동등하다.
    • 하지만 f(x)⋅g(x)f(x)\cdot g(x)를 x, y쌍 형태에서는 그냥 원소별로 곱해주면 된다!
  • FFT는 특정 성질을 띠는 xx들을 선택해, 이 두 형태간의 변환을 O(nlg⁡n)O(n \lg n)에 수행한다.
  • 곱셈 자체는 O(n)O(n)이다.
  • 자세히는 wookayin님의 슬라이드를 보자:

C++ 구현:

#include<vector>
#include<complex>
#include<cmath>

using namespace std;

typedef complex<double> Complex;
typedef vector<Complex> ComplexVector;
typedef vector<int> Polynomial;

const double PI = 2.0 * acos(0.0);

// Given a n-th polynomial p, return its values at
// w^0, w^1, .., w^(n-1). n is assumed to be a power of 2.
// Since the size of the input and output are the same, the output is stored at
// p.
void dft(ComplexVector& p, Complex w) {
  int n = p.size();
  if(n == 1) return;

  // divide
  ComplexVector even(n / 2), odd(n / 2);
  for(int i = 0; i < n/2; ++i) {
    even[i] = p[i * 2];
    odd[i] = p[i * 2 + 1];
  }

  // conquer
  dft(even, w * w); 
  dft(odd, w * w);

  // merge
  Complex w_power = 1;
  for(int i = 0; i < n/2; ++i) {
    Complex offset = w_power * odd[i];
    p[i      ] = even[i] + offset;
    p[i + n/2] = even[i] - offset;
    w_power *= w;
  }
}


// returns smallest power of 2 s.t. p2 >= n.
int roundUp(int n) {
  int p2 = 1;
  while(p2 < n) p2 *= 2;
  return p2;
}

Polynomial operator * (const Polynomial& a, const Polynomial& b) {
  // last *2 is needed because C can have twice the degree from original polys
  int n = roundUp(max(a.size(), b.size())) * 2;

  // Complex representations of a and b
  ComplexVector ac(a.begin(), a.end()), bc(b.begin(), b.end());
  ac.resize(n); 
  bc.resize(n);

  // FFT 
  Complex w = polar(1.0, 2 * PI / n);
  dft(ac, w);
  dft(bc, w);
  // Pointwise multiplication
  for(int i = 0; i < n; ++i) 
    ac[i] *= bc[i];

  // Inverse FFT
  dft(ac, polar(1.0, -2 * PI / n));
  for(int i = 0; i < n; ++i) 
    ac[i] /= double(n);

  // Trim zero paddings
  while(!ac.empty() && fabs(real(ac.back())) < 1e-9) 
    ac.pop_back();

  // return real
  Polynomial ret(ac.size());
  for(int i = 0; i < ac.size(); ++i) 
    ret[i] = int(round(real(ac[i])));

  return ret;
}

긴 정수 곱셈의 응용

알면 유용한 사실들

  • 약수의 상한: [1..n][1..n]의 범위에 대하여 최대 약수의 개수는 O(n1/3)O(n^{1/3})으로 어림잡을 수 있다. OEIS66150을 참고하면 10910^9범위 내에서는 최대 1344개, 101810^{18}범위 내에서는 최대 103680개의 약수가 있다. 각각 735134400, 897612484786617600이 그에 해당한다. 관련문제
  • 원점에서 (a,b)까지 선분 위 격자점의 개수는 gcd(a,b)
  • pi(x) ~= x/log(x)
  • 2차원에서 L1L_1 길이와 L∞L_\infty 길이는 45도 돌리고 scaling하면 같게 할 수 있다.
  • homogenous coordinate system: 한 차원을 추가하고 상수를 곱해서 같게 할 수 있는 것들을 동등하게 보는 것으로 기하를 다룰 수 있다. (관련 글 링크)
    • 2차원 기하
      • 점 (x,y)(x,y)를 (kx,ky,k)(kx,ky,k)로 표현하고 직선 ax+by+c=0ax+by+c = 0을 (a,b,c)(a,b,c)로 표현하면 a(kx)+b(ky)+c(k)=0a(kx)+b(ky)+c(k) = 0, 즉 (kx,ky,k)⋅(a,b,c)=0(kx,ky,k)\cdot(a,b,c)=0에서 duality를 얻는다. 점의 경우 세번째 성분이 1이 되도록 어떤 실수를 scalar 곱을 해서 해석하면, 원래 알고 있는 것이 나온다. 예를 들어 (2,4,2)는 (1,2)로 해석하는 식이다. 점을 나타내는 좌표의 세 번째 성분이 0인 경우 무한히 멀리 떨어진 해당 방향의 점으로 여긴다.
      • 점과 직선은 자유롭게 관점을 바꿔보아도 여러 관계가 유지된다. 점과 점을 지나는 직선은 관점을 바꾸어 직선과 직선을 지나는 점이라고 볼 수 있다. 예를 들어 (1,2)(1,2)과 (2,3)(2,3)를 지나는 y−x−1=0y-x-1=0이라는 직선은 y+2x+1=0y+2x+1=0, 2y+3x+1=02y+3x+1=0을 지나는 (−1,1)(-1,1)이라고 여길 수 있다.
      • 위 내적이 있는 식은 수직을 의미하는 관계이므로, 두 점 (x1,y1)(x_1,y_1), (x2,y2)(x_2,y_2)을 지나는 직선은 (x1,y1,1)×(x2,y2,1)(x_1, y_1, 1) \times (x_2, y_2, 1)로 얻을 수 있다. 예를 들어 (1,2)(1,2)와 (2,3)(2,3)을 지나는 직선은 (1,2,1)×(2,3,1)=(−1,1,1)(1,2,1) \times (2,3,1) = (-1, 1, 1)에서 −x+y+1=0-x+y+1=0을 얻는다. duality에 의해 직선과 직선의 교점도 외적으로 얻는다. 두 점/직선을 교차하는 직선/점이 없거나 무한히 많은 경우 재밌는 결과가 나오므로 직접 확인해보자.
    • 3차원 기하
      • 2차원과 마찬가지로 점 (x,y,z)를 (kx,ky,kz,k)로 표현한다. 그리고 함께 다루는 것은 평면 ax+by+cz+d = 0을 의미하는 (a,b,c,d)이다. 직선은 평면 두 개를 이용해 표현한다.
      • wedge product를 쓰는 것이 있다.
      • 점/평면 세 개 (a1,b1,c1,d1),⋯,(a3,b3,c3,d3)(a_1, b_1, c_1, d_1), \cdots, (a_3, b_3, c_3, d_3)의 공통평면/교점은 |e1e2e3e4a1b1c1d1a2b2c2d2a3b3c3d3|\left| \begin{matrix} e_1 & e_2 & e_3 & e_4 \\ a_1 & b_1 & c_1 & d_1 \\ a_2 & b_2 & c_2 & d_2 \\ a_3 & b_3 & c_3 & d_3 \end{matrix} \right|로 계산할 수 있다. 여기서 eie_i는 ii번째 단위 벡터를 나타낸다. 참고: http://www.cs.iastate.edu/~cs577/handouts/homogeneous-coords-space.pdf
      • wedge product 개념을 이용하면 점, 직선, 평면들의 관계를 쉽게 계산할 수 있다.
Code-Test, Algorithm
algorithm math
This post is licensed under CC BY 4.0 by the author.
Contents

Deep-Learning Computer-Vision Guide Notes[2]

[lvl2][2022 KAKAO TECH INTERNSHIP]두 큐 합 같게 만들기