T-SNE (t-distributed stochastic neighbor embedding)

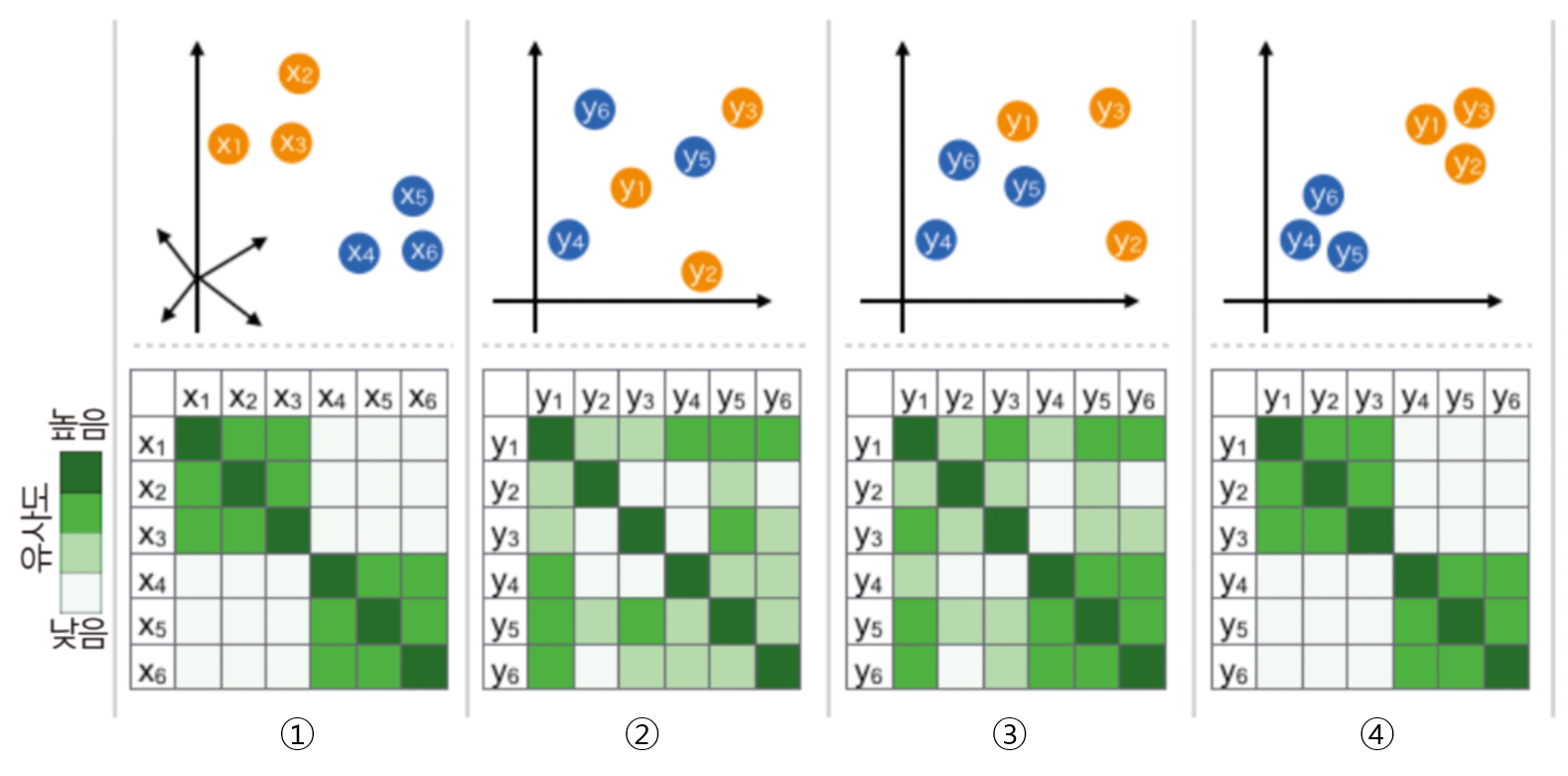
t-SNE는 PCA와 다르게 비선형 차원분석

Dimensionality Reduction의 의미

• 수많은 feature들을 가지고 있는 데이터셋에서 feature들 간의 관계를 파악하기가 어렵다
• feature의 수가 너무 많으면 머신 러닝 모델의 성능을 저하시키곤 하고 overfit을 발생시킨다
• dimensionality reduction(차원 축소)는 중요한 feature의 갯수는 남기고 불필요한 feature의 갯수를 줄이는 데 사용되곤 한다

효과

• feature들 간의 관계를 줄일 수 있다
• feature을 2D, 3D로 시각화를 가능하게 한다
• overfit을 방지

방법:

1.  Feature Elimination
   • Feature를 단순히 삭제하는 방법
   • 간단하나 삭제된 feature들로 부터 어떠한 정보를 얻지는 못한다는 단점 존재(information loss)
2. Feature Selection
   • 통계적인 방법을 이용하여 feature들의 중요도에 rank를 부여
   • information loss가 발생할 수 있으며 동일한 문제를 푸는 다른 데이터셋에서는 다른 rank를 매길 수 있다는 문제가 있을 수 있다
3. Feature Extraction
   • 새로운 독립적인 feature를 만드는 방법
   • 새로 만들어진 feature는 기존에 존재하였던 독립적인 feature들의 결합으로 만들어 짐
   • linear한 방법과 non-linear한 방법이 있다

t-SNME의 의미

• 높은 차원의 복잡한 데이터를 2차원에 차원 축소하는 방법
• 높은 차원 공간에서 비슷한 데이터 구조는 낮은 차원 공간에서 가깝게 대응하며, 비슷하지 않은 데이터 구조는 멀리 떨어져 대응된다 → 데이터 구조를 이해하는 데 도움

t-SNE의 수식적 의미

1. t-SNE 알고리즘은 고차원 공간에서의 점들의 유사성과 그에 해당하는 저차원 공간에서의 점들의 유사성을 계산
2. 점들의 유사도는 A를 중심으로 한 정규 분포에서 확률 밀도에 비례하여 이웃을 선택하면 포인트 A가 포인트 B를 이웃으로 선택한다는 조건부 확률로 계산
3. 저 차원 공간에서 데이터 요소를 완벽하게 표현하기 위해 고차원 및 저 차원 공간에서 이러한 조건부 확률 (또는 유사점) 간의 차이를 최소화하려고 시도
4. 조건부 확률의 차이의 합을 최소화하기 위해 t-SNE는 gradient descent 방식을 사용하여 전체 데이터 포인트의 KL-divergence 합계를 최소화
   • Kullback-Leibler divergence 또는 KL divergence는 한 확률 분포가 두 번째 예상 확률 분포와 어떻게 다른지 측정하는 척도

• 정리하면 t-SNE는 두가지 분포의 KL divergence를 최소화 한다.
  • 입력 객체(고차원)들의 쌍으로 이루어진 유사성을 측정하는 분포
  • 저차원 점들의 쌍으로 유사성을 측정하는 분포

  

하지만 t-SNE 과정이 끝나면 input feature를 확인하기가 어렵고 t-SNE 결과만 가지고 무언가를 추론 하기는 어려움이 있기 때문에 주로 시각화 툴로 사용된다

t-분포

• t-SNE는 정규분포 대신 t-분포를 사용
• 소 표본 (n < 30)으로 모 평균 추정하고 모집단이 정규분포와 유사함을 알고 있으나 모 표준편차를 모를 때 주로 사용

t 분포의 이름은 Student 라는 가명을 사용한 이름의 학자가 발표한 Student t-분포에서 유래

특징

• 표준 정규부높와 유사하게 0을 평균으로 가지고 대칭적인 형태를 가짐
• 표준 정규분포에 비해 분산이 큼(평평하고 꼬리가 김(양쪽 꼬리 형태가 두터운 형태))
• 정규분포는 평균과 분산에 따라 형태가 달라지는 반면, t-분포는 카이 제곱 분포와 같이 자유도에 따라 모양이 달라짐
• $자유도 = 표본의 수 - 1$
• 자유도가 커질수록 표준 정퓨분포에 가까워짐
  • 자유도가 30이 넘으면 정규분포와 비슷하기 떄문에 t-분포는 자유도 30이하에서 주로 사용

Code

from sklearn.manifold import TSNE

tsne= TSNE(n_components=2,
		   verbose=1,
		   learning_rate=1000,
		   perplexity=100,
		   n_iter=1000)
tsne_result = tsne.fit_transform(train_feature_reduced)

parameter 설명

• n_components(Default = 2): 줄일 목표 차원수
• verbose
• learning_rate: ML의 기초적인 파라미터. 높으면 빠르지만 최솟값을 찾기가 힘들고 낮으면 너무 느리다. Default = 200 이지만 주로 10~1000까지 사용된다.
• perplexity(Default = 30): 복잡도에 관련된 파라미터로 이웃 간에 거리에 대한 파라미터이다. 너무 높이면 거의 한점 처럼보이고 너무 낮으면 cluster를 잘 시키기 힘들다. Default = 30으로 5~50를 쓴다. 실제로 cluster를 잘 시키기 위해 200이상으로 높혔더니 정말 형체가 사라졌다.
• n_iter: 몇 번 돌릴 것인지에 대한 파라미터. Default = 1000이다. 너무 적게 돌리면 의미가 없기 때문에 250이상을 쓰라고 나와있다.

참고: https://velog.io/@swan9405/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-T-SNE-T-distributed-Stochastic-Neighbor-Embedding

https://gaussian37.github.io/ml-concept-t_sne/#