Syshin

T-SNE (t-distributed stochastic neighbor embedding)

8 min read

Summary

t-SNE(t-distributed stochastic neighbor embedding)는 고차원 데이터를 2차원이나 3차원으로 축소하는 비선형 차원 축소 기법이다. PCA와 달리 비선형적 관계를 보존하며, 고차원 공간에서 비슷한 데이터 포인트는 저차원에서도 가깝게, 다른 포인트는 멀리 배치한다. 알고리즘은 두 차원 공간 간의 조건부 확률 분포의 KL-divergence를 최소화하는 방식으로 작동하며, 복잡한 데이터 구조의 시각화에 특히 유용하다.

개요

t-SNE(t-distributed stochastic neighbor embedding)는 복잡한 고차원 데이터를 시각화하기 위한 강력한 비선형 차원 축소 기법이다. PCA와 같은 선형 차원 축소 방법과 달리, t-SNE는 데이터의 비선형적 관계를 효과적으로 보존할 수 있다.

t-SNE 차원 축소 예시

차원 축소(Dimensionality Reduction)의 필요성

수많은 특성(feature)을 가진 데이터셋에서는 다음과 같은 문제가 발생한다:

  • 특성들 간의 복잡한 관계를 파악하기 어려움
  • 특성이 너무 많으면 머신러닝 모델의 성능 저하 및 과적합 발생
  • 고차원 데이터의 시각화가 어려움

이러한 문제를 해결하기 위해 차원 축소 기법이 사용된다.

차원 축소의 효과

  • 특성들 간의 관계를 단순화
  • 데이터를 2D 또는 3D로 시각화 가능
  • 과적합(overfitting) 방지
  • 모델 훈련 시간 단축

차원 축소 방법

  1. 특성 제거(Feature Elimination)

    • 특성을 단순히 삭제하는 방법
    • 간단하지만 삭제된 특성의 정보 손실(information loss) 발생

  2. 특성 선택(Feature Selection)

    • 통계적 방법을 이용하여 특성의 중요도에 순위 부여
    • 정보 손실 가능성이 있으며, 다른 데이터셋에서는 다른 순위가 매겨질 수 있음

  3. 특성 추출(Feature Extraction)

    • 새로운 독립적인 특성을 생성하는 방법
    • 기존 특성들의 조합으로 만들어짐
    • 선형(예: PCA)과 비선형(예: t-SNE) 방법으로 구분

t-SNE의 개념과 원리

t-SNE는 고차원 데이터를 2차원이나 3차원으로 축소하여 시각화하는 기법으로, 다음과 같은 특징을 가진다:

  • 고차원 공간에서 비슷한 데이터 구조는 저차원 공간에서도 가깝게 배치
  • 비슷하지 않은 데이터 구조는 저차원 공간에서 멀리 배치
  • 국소적 구조(local structure)를 잘 보존하는 경향이 있음

t-SNE의 수학적 원리

t-SNE 알고리즘은 다음과 같은 과정으로 작동한다:

  1. 고차원 공간에서 점들 간의 유사성을 조건부 확률로 계산

    • 점 A를 중심으로 한 정규 분포에서 점 B를 이웃으로 선택할 확률

  2. 저차원 공간에서도 점들 간의 유사성을 조건부 확률로 계산

    • 저차원에서는 Student t-분포(자유도 1)를 사용

  3. 두 확률 분포 간의 차이(KL-divergence)를 최소화

    • Kullback-Leibler divergence는 한 확률 분포가 다른 확률 분포와 얼마나 다른지 측정하는 지표
    • 경사 하강법(gradient descent)를 사용하여 KL-divergence 합계를 최소화

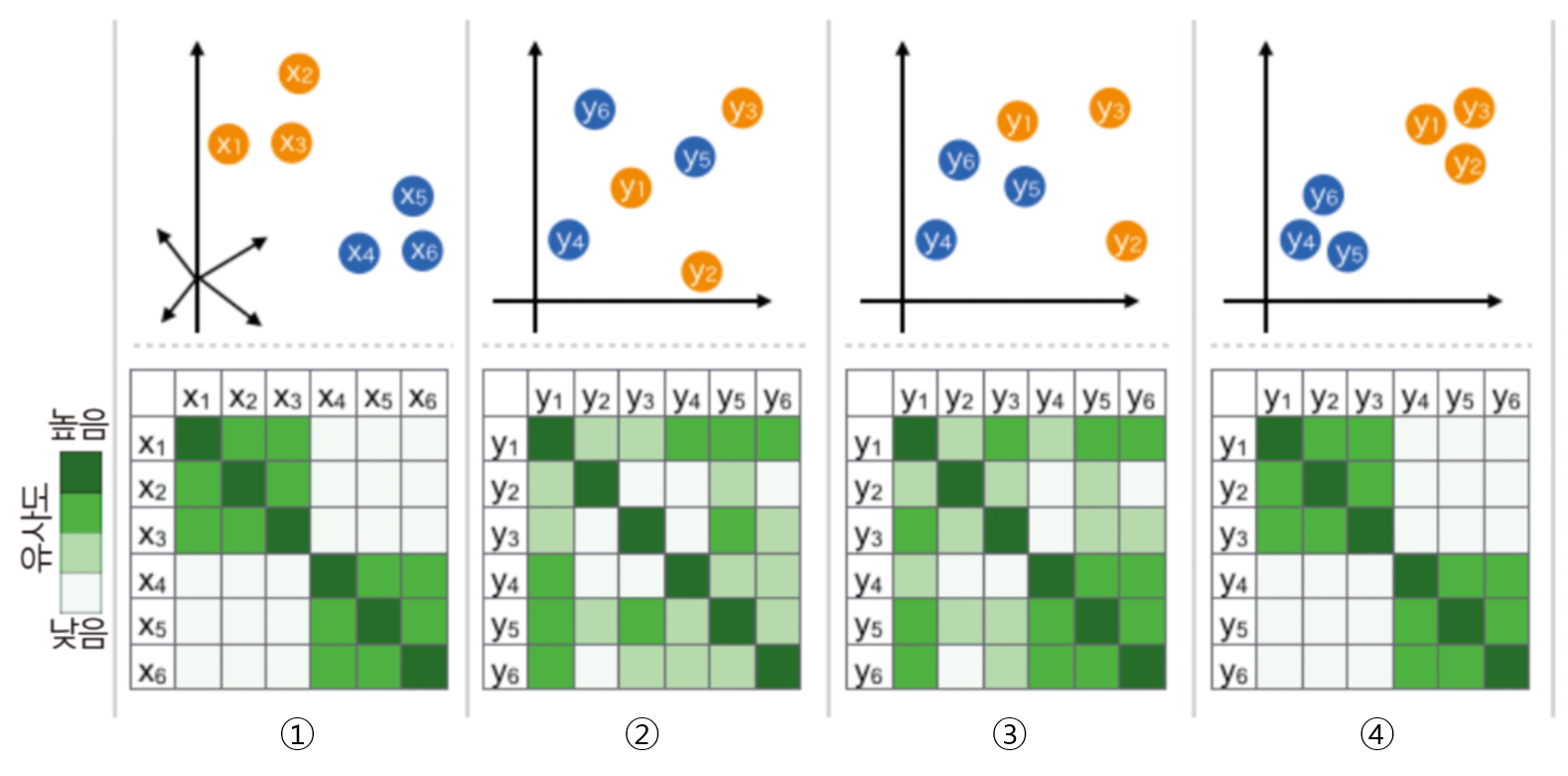
t-SNE 수학적 원리

t-SNE의 주요 매개변수

t-SNE 알고리즘에는 결과에 큰 영향을 미치는 몇 가지 중요한 매개변수가 있다:

1. perplexity

  • 효과적인 이웃의 수를 결정하는 매개변수
  • 일반적으로 5-50 사이의 값을 사용
  • 데이터셋 크기에 따라 적절한 값을 선택해야 함

2. 학습률(learning rate)

  • 경사 하강법의 스텝 크기를 결정
  • 너무 높으면 불안정해지고, 너무 낮으면 수렴이 느림

3. 반복 횟수(iterations)

  • 알고리즘이 실행되는 횟수
  • 일반적으로 250-1000회 사용
  • 너무 적으면 최적화가 충분히 이루어지지 않음

t-SNE 활용 사례

t-SNE는 다양한 분야에서 고차원 데이터 시각화에 활용된다:

  • 이미지 데이터: MNIST 손글씨 데이터셋, 얼굴 인식 데이터 시각화
  • 유전체 데이터: 유전자 발현 데이터 분석
  • 자연어 처리: 단어 임베딩 시각화
  • 네트워크 데이터: 소셜 네트워크 구조 시각화

t-SNE는 이상 탐지(Anomaly Detection) 분야에서도 유용하게 활용될 수 있다. 고차원 데이터에서 정상 패턴과 이상 패턴을 시각적으로 분리하여 분석할 수 있기 때문이다.

t-SNE의 장단점

장점

  • 비선형 데이터의 국소적 구조를 잘 보존
  • 군집(cluster)을 시각적으로 잘 분리
  • 복잡한 고차원 데이터에 대한 직관적 이해 제공

단점

  • 계산 비용이 높음(O(n²))
  • 전역적 구조(global structure)는 잘 보존하지 못할 수 있음
  • 결과가 초기화와 매개변수에 민감함
  • 새로운 데이터 포인트에 대한 변환 어려움(out-of-sample extension 문제)

이러한 단점을 보완하기 위해 다른 차원 축소 기법과 함께 사용하거나, UMAP과 같은 최신 기법을 고려할 수 있다.

결론

t-SNE는 고차원 데이터의 시각화에 매우 유용한 비선형 차원 축소 기법이다. 특히 군집 구조를 시각적으로 잘 표현하여 데이터의 패턴을 이해하는 데 도움을 준다. 다만, 계산 비용이 높고 매개변수 설정에 민감하다는 단점이 있다.

t-SNE를 효과적으로 활용하려면 데이터의 특성과 시각화의 목적을 명확히 하고, 적절한 매개변수를 설정하는 것이 중요하다. 불균형 데이터 예측과 같은 복잡한 문제에서도 t-SNE를 통한 시각화가 중요한 통찰력을 제공할 수 있다.

최신 연구에서는 t-SNE의 단점을 보완하는 UMAP과 같은 새로운 기법들이 개발되고 있으나, t-SNE는 여전히 데이터 시각화의 중요한 도구로 널리 사용되고 있다.

Graph View

Backlinks